Fonction continue
Topologie
Intuitivement, fonction dont la courbe n’est interrompue nulle part. On peut en tracer le graphique sans lever le crayon. Même si une fonction continue sur un intervalle [a, b] doit être définie pour tout élément de cet intervalle, il faut aussi mentionner que son image doit aussi ne présenter aucune discontinuité.
« La fonction f définie par la relation f(x) = −2x² + 4 sur l’intervalle [-1, 1] est une fonction continue. »
IMAGE EN LANGUE DES SIGNES :
 f
f
 o
o
 n
n
 c
c
 t
t
 i
i
 o
o
 n
n
 c
c
 o
o
 n
n
 t
t
 i
i
 n
n
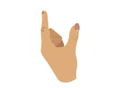 u
u
 e
e
Sürekli Fonksiyon
Topoloji
Sezgisel olarak, sürekli bir fonksiyon; grafiği boyunca hiçbir kopukluk ya da kesinti içermeyen fonksiyondur. Böyle bir fonksiyonun grafiği, kalemi kâğıttan kaldırmadan çizilebilir. Matematiksel olarak, bir fonksiyonun [a, b] kapalı aralığında sürekli olabilmesi için şu iki koşulu sağlaması gerekir: 1. Fonksiyon, bu aralıktaki her x \in [a, b] için tanımlı olmalıdır. 2. Fonksiyonun bu aralıktaki görüntüsü, yani değer kümesi, herhangi bir noktada süreksizlik (discontinuité) göstermemelidir. Bu koşullar sağlandığında, fonksiyonun hem tanım kümesinde hem de değer kümesinde süreklilikten söz edilir.
"None"
İŞARET DİLİYLE GÖSTERİMİ :
 s
s
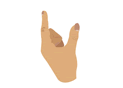 ü
ü
 r
r
 e
e
 k
k
 l
l
 i
i
 f
f
 o
o
 n
n
 k
k
 s
s
 i
i
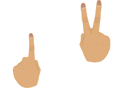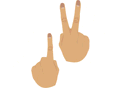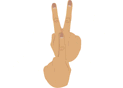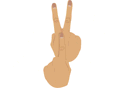 y
y
 o
o
 n
n
