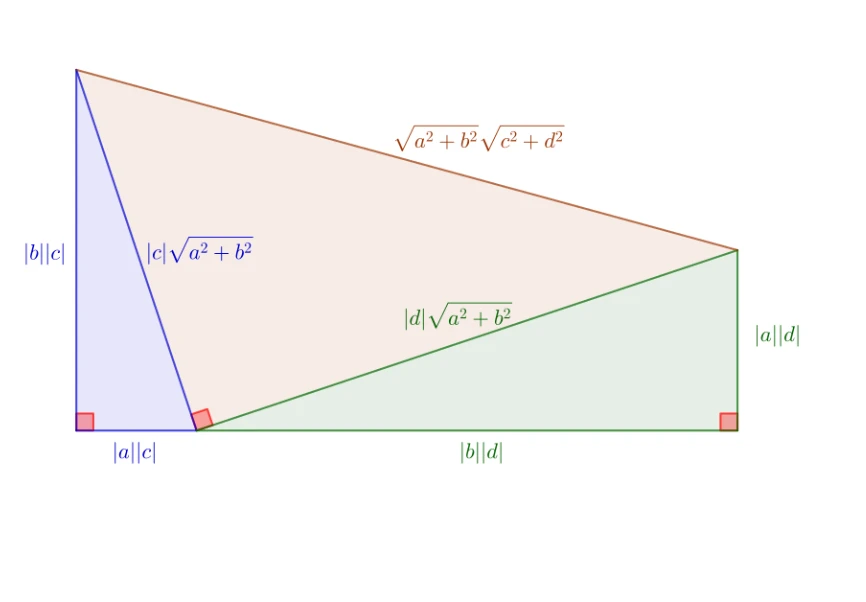Cauchy-Schwarz eşitsizliği (bazen Schwarz eşitsizliği veya Cauchy eşitsizliği veya Cauchy-Schwarz-Bunyakovski eşitsizliği olarak anılır) matematikte önemli bir eşitsizliktir. Özellikle lineer cebir, analiz, istatistik ve olasılık kuramında bu eşitsizlik yoğun bir şekilde kullanılmaktadır. Toplamlar için bu eşitsizlik ilk defa Augustin Louis Cauchy tarafından 1821'de ve integraller için ise bu eşitsizlik ilk defa Viktor Bunyakovski tarafından 1850'de ve sonra yine Hermann Amandus Schwarz tarafından 1888'de ortaya atılmıştır. Eşitsizliğin ifadesi Cauchy-Schwarz eşitsizliğine göre bir iç çarpım uzayında bulunan tüm x {\displaystyle x} ve y {\displaystyle y} öğeleri için şu ifade geçerlidir: | ⟨ x , y ⟩ | 2 ≤ ⟨ x , x ⟩ ⋅ ⟨ y , y ⟩ . {\displaystyle |\langle x,y\rangle |^{2}\leq \langle x,x\rangle \cdot \langle y,y\rangle .} Burada, ⟨ ⋅ , ⋅ ⟩ {\displaystyle \langle \cdot ,\cdot \rangle } iç çarpımı temsil etmektedir. Bu ifadenin her iki tarafının karekökü alınırsa ‖ u ‖ := ⟨ u , u ⟩ , {\displaystyle \|\mathbf {u} \|:={\sqrt {\langle \mathbf {u} ,\mathbf {u} \rangle }},}norm tanımı kullanılarak aynı özdeş şekilde yeni bir ifade ile şöyle yazılır: | ⟨ x , y ⟩ | ≤ | | x | | ⋅ | | y | | . {\displaystyle |\langle x,y\rangle |\leq ||x||\cdot ||y||.} Buna ek olarak ifadenin iki tarafının birbirine eşit olması ancak ve ancak x {\displaystyle x} ve y {\displaystyle y} öğelerinin birbirlerine lineer olarak bağımlı olmaları halinde gerçekleşir. Öte yandan aynı eşitsizlik x 1 , x 2 , … , x n {\displaystyle x_{1},x_{2},\dots ,x_{n}} ve y 1 , y 2 , … , y n {\displaystyle y_{1},y_{2},\dots ,y_{n}} reel sayıları için ( ∑ i = 1 n x i 2 ) ( ∑ i = 1 n y i 2 ) ≥ ( ∑ i = 1 n x i y i ) 2 {\displaystyle (\sum _{i=1}^{n}x_{i}^{2})(\sum _{i=1}^{n}y_{i}^{2})\geq (\sum _{i=1}^{n}x_{i}y_{i})^{2}} olarak yazılabilir. Eşitlik sadece x 1 y 1 = x 2 y 2 = ⋯ = x n y n {\displaystyle {\frac {x_{1}}{y_{1}}}={\frac {x_{2}}{y_{2}}}=\dots ={\frac {x_{n}}{y_{n}}}} için sağlanır. Kanıt İç çarpımın tanımı gereği, herhangi iç çarpım uzayındaki x {\displaystyle \mathbf {x} } ve y {\displaystyle \mathbf {y} } öğesi için, y = 0 {\displaystyle \mathbf {y} =0} ise, eşitlik vardır: 0 = | ⟨ x , 0 ⟩ | | = | x | | | | 0 | | . {\displaystyle 0=|\langle \mathbf {x} ,0\rangle ||=|\mathbf {x} ||\ ||0||.} y ≠ 0 {\displaystyle \mathbf {y} \neq 0} ise, o zaman z := x − ⟨ x , y ⟩ ⟨ y , y ⟩ y {\displaystyle \mathbf {z} :=\mathbf {x} -{\frac {\langle \mathbf {x} ,\mathbf {y} \rangle }{\langle \mathbf {y} ,\mathbf {y} \rangle }}\mathbf {y} } alalım. İç çarpımın doğrusallığından, ⟨ z , y ⟩ = ⟨ x − ⟨ x , y ⟩ ⟨ y , y ⟩ y , y ⟩ = ⟨ x , y ⟩ − ⟨ x , y ⟩ ⟨ y , y ⟩ ⟨ y , y ⟩ = 0 {\displaystyle \langle \mathbf {z} ,\mathbf {y} \rangle =\left\langle \mathbf {x} -{\frac {\langle \mathbf {x} ,\mathbf {y} \rangle }{\langle \mathbf {y} ,\mathbf {y} \rangle }}\mathbf {y} ,\mathbf {y} \right\rangle =\langle \mathbf {x} ,\mathbf {y} \rangle -{\frac {\langle \mathbf {x} ,\mathbf {y} \rangle }{\langle \mathbf {y} ,\mathbf {y} \rangle }}\langle \mathbf {y} ,\mathbf {y} \rangle =0}olduğu görülür. Yani, z {\displaystyle \mathbf {z} } y {\displaystyle \mathbf {y} }'ye diktir. O zaman, x = ⟨ x , y ⟩ ⟨ y , y ⟩ y + z {\displaystyle \mathbf {x} ={\frac {\langle \mathbf {x} ,\mathbf {y} \rangle }{\langle \mathbf {y} ,\mathbf {y} \rangle }}\mathbf {y} +\mathbf {z} }yazılıp, iç çarpımda geçerli olan Pisagor teoremi uygulanabilir. Gerçekten de, ‖ x ‖ 2 = | ⟨ x , y ⟩ ⟨ y , y ⟩ | 2 ‖ y ‖ 2 + ‖ z ‖ 2 = | ⟨ x , y ⟩ | 2 ( ‖ y ‖ 2 ) 2 ‖ y ‖ 2 + ‖ z ‖ 2 = | ⟨ x , y ⟩ | 2 ‖ y ‖ 2 + ‖ z ‖ 2 ≥ | ⟨ x , y ⟩ | 2 ‖ y ‖ 2 . {\displaystyle \|\mathbf {x} \|^{2}=\left|{\frac {\langle \mathbf {x} ,\mathbf {y} \rangle }{\langle \mathbf {y} ,\mathbf {y} \rangle }}\right|^{2}\|\mathbf {y} \|^{2}+\|\mathbf {z} \|^{2}={\frac {|\langle \mathbf {x} ,\mathbf {y} \rangle |^{2}}{(\|\mathbf {y} \|^{2})^{2}}}\,\|\mathbf {y} \|^{2}+\|\mathbf {z} \|^{2}={\frac {|\langle \mathbf {x} ,\mathbf {y} \rangle |^{2}}{\|\mathbf {y} \|^{2}}}+\|\mathbf {z} \|^{2}\geq {\frac {|\langle \mathbf {x} ,\mathbf {y} \rangle |^{2}}{\|\mathbf {y} \|^{2}}}.}Eşitsizliğin diğer formu için ise ispat şöyle yapılabilir: x 1 , x 2 , … , x n , y 1 , y 2 , … , y n {\displaystyle x_{1},x_{2},\dots ,x_{n},y_{1},y_{2},\dots ,y_{n}} reel sayıları için ( x 1 2 + x 2 2 + ⋯ + x n 2 ) x 2 + 2 ( x 1 y 1 + x 2 y 2 + ⋯ + x n y n ) x + ( y 1 2 + y 2 2 + ⋯ + y n 2 ) = ∑ i = 1 n [ x i 2 x 2 + 2 x i y i x + y i 2 ] = ∑ i = 1 n ( x i x + y i ) 2 ≥ 0 {\displaystyle (x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2})x^{2}+2(x_{1}y_{1}+x_{2}y_{2}+\dots +x_{n}y_{n})x+(y_{1}^{2}+y_{2}^{2}+\dots +y_{n}^{2})=\sum _{i=1}^{n}[x_{i}^{2}x^{2}+2x_{i}y_{i}x+y_{i}^{2}]=\sum _{i=1}^{n}(x_{i}x+y_{i})^{2}\geq 0}olduğu görülür. En soldaki ifade ikinci dereceden bir polinom olup negatif değildir. Bu yüzden bu polinomun diskriminantı pozitif olamaz. Yani B 2 − 4 A C ≤ 0 ⇒ ( 2 ( ∑ i = 1 n x i y i ) ) 2 ≤ 4 ( ∑ i = 1 n x i 2 ) ( ∑ i = 1 n y i 2 ) ⇒ ( ∑ i = 1 n x i y i ) 2 ≤ ( ∑ i = 1 n x i 2 ) ( ∑ i = 1 n y i 2 ) {\displaystyle B^{2}-4AC\leq 0\Rightarrow (2(\sum _{i=1}^{n}x_{i}y_{i}))^{2}\leq 4(\sum _{i=1}^{n}x_{i}^{2})(\sum _{i=1}^{n}y_{i}^{2})\Rightarrow (\sum _{i=1}^{n}x_{i}y_{i})^{2}\leq (\sum _{i=1}^{n}x_{i}^{2})(\sum _{i=1}^{n}y_{i}^{2})} olur ve ispat tamamlanır.